数学日记——大自然的数学奥秘 三年级4班 湛浩天

      暑假，我参加了盼望已久的徽州游学营。一路上，我学习设计、搭建古建筑、制墨、烧陶、做版画、造纸伞、登黄山，勘查了西溪南生态湿地的枫杨林，夜观了古村田野间的植物和昆虫，渡过了难忘的7天。让我印象深刻的是，每一个环节都充满有趣的数学元素，真是7天7夜都说不完！ 

    枫杨林和斐波那契数列

    我们住在西溪南湿地，窗外是一片美丽的枫杨林。枫杨树是湿地特有的植物，看，如果我不告诉你，你是不是以为我手心里是一只小飞蛾？实际上它是枫杨树的种子！

      这片美丽的枫杨林是自然形成的，绿树成荫，遮挡了烈日，带给我们清凉的快乐。我抬头看树枝，为什么每一根树枝都长满了绿叶，每一片绿叶都充分吸收了阳光，既没有遮挡别的绿叶，又没有被 别的绿叶遮挡，好像很聪明的样子？这个奥秘，竟然被斐波那契数列解开了。

       意大利比萨市的莱昂纳多的父亲Guglielmo Bonaccio是一名海关官员，“斐波纳契”是拉丁语“弗立维.波纳切”的缩写，意思是“Bonaccio之子”。莱昂纳多年轻时候就发现阿拉伯数字0-9比那时欧洲常用的罗马数字I, V, X更好用，就用阿拉伯数字表示兔子数列。这个数列来源于自然界兔子的繁殖记录：一雌一雄的一对小兔子放在一起，第一个月时还没有长大，不会生小兔，所以兔子的对数是1；第二个月还没有生小兔，对数还是1；第三个月生了一对小兔，兔子总对数变成2；第四个月，会生的继续生了一对，不会生的没有生，一共有1+2=3对兔子；第五个月，2+3=5对兔子……以此类推，用阿拉伯数字写出来就是1，1，2，3，5，8，13，21，34，55……其中每个数字都是前面两个相邻数字的和。19世纪，法国数学家爱都华.卢卡斯为了纪念莱昂纳多的贡献，将他用阿拉伯数字列出的兔子数列命名为“斐波纳契数列” (Fibonacci sequence)。

     枫杨树在生长过程中，新生的枝条像小兔子一样，需要时间长大，才能萌发新枝，所以，一株树苗在一段间隔比如一年以后长出一条新枝，第二年新枝“休息”，老枝继续长，第三年，老枝与去年“休息”的枝都长，当年生的新枝遵守同样的自然规则第二年“休息”。这样，一株树木每年的枝条总数，就组成了和兔子数列一样的斐波那契数列，这就是生物学著名的“鲁德维格定律” (Ludvig law)。 枫杨树叶子的生长也是这样，每片叶子为了在生长的过程中最好利用空间，既不遮住别的叶子，又不被别的叶子遮住，每片叶子和前一片叶子之间的角度是 222.5°，这样排列，枫杨树能最充分地利用阳光和空气，繁衍更多后代。这个角度称为“黄金角度”，因为它和整个圆周 360° 之比是黄金分割数0.618的倒数，而这种生长方式符合斐波那契螺旋的图案。

蝉的冬眠和质数

    一天晚上，我们带上手电筒，做好防蚊措施，跟着老师去夜探。田野里真是“稻花香里说丰年，听取蛙声一片”，除了蛙声，还有蝉的声音。老师问我们：“蝉在树上，你们知道蝉的幼虫在哪儿吗？”我迫不及待地答到：“我在《法布尔昆虫记》里读到过，蝉的幼虫在地下！”

       “那你知道吗？如果‘数学’可以被当作形容词，蝉真是种很‘数学’的生物！”

       长成成虫前的蝉会在地下度过一个漫长的幼虫期，钻出地面后，只能活几十天，也就是说，蝉的生命周期基本上等于它们在地下的幼虫期。不同种类的蝉在地下生活的时间也就是它们的生命周期不同，有2年、3年、5年、13年、17年不等，神奇的是，它们的生命周期都是质数！为什么蝉的生命周期是质数而不是合数呢？这是巧合吗？

       老师说，如果蝉的天敌生命周期是2年，天敌在第2、4、6年像这样每2年会大量出现一次，那一年钻出土壤的蝉碰到天敌的几率很高，容易被吃掉同样，如果天敌的生命周期是3或5年，第3、5、3*2=6、5*2=10年这样每3年或每5年钻出土壤的蝉就会碰到天敌。也就是说，如果蝉和天敌的生命周期一样，被吃掉的几率就很大，也无法繁衍后代，影响整个种族的数量。如果蝉的天敌生命周期是蝉生命周期的因子，蝉被吃掉的几率会更大，比如，生命周期是15年蝉钻出土壤时，不仅会遇到生命周期是15年的天敌，还会遇到生命周期为15/5=3年和15/3=5年的天敌，而且下一次这种15年蝉钻出土壤时，一定还有同样的遭遇，这样整个种族就很容易灭绝。但假如生命周期为17年的蝉今年钻出土壤时遇到生命周期为3年的天敌，那么下次与这种天敌碰面的时候就是17*3=42年后了，中间还有两次钻出土壤，安全繁衍下一代的机会。因此，从下面这张表可以看出来，以质数作为生命周期的蝉，种族存活率会大幅提升，能最大几率地在自然界中存活下来。

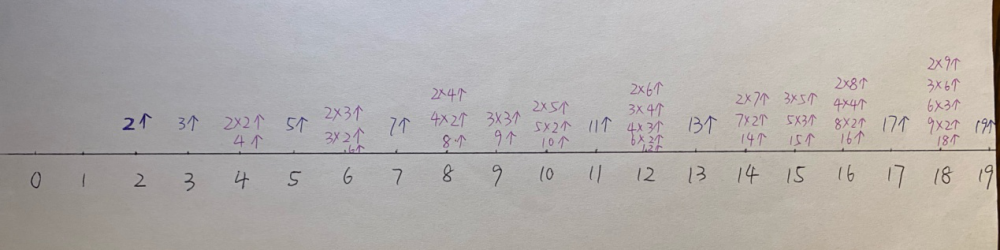
        我越来越深深地感受到数学的美。生活和大自然中的数学，那么广泛又那么细致入微。人们用数学创造着世界，而大自然用数学创造着地球。