从一位到2000万亿位：如何计算π 六年级（4）班  张沛铨

从一位到2000万亿位：如何计算π

六年级（4）班  张沛铨

        在知道如何计算π之前，我们需要知道所谓π是什么。π就是一个圆的周长和直径的比值。

        但是，对于算π的方法，我就有所误解。我有一段时间一直以为π非常易算：就直接用软尺量一下圆的周长再量一下圆的直径，再用周长除以直径，是不是就可以了呢？我验证过：我自己画了一个圆，再用软尺量了它的周长和直径。我自己做了除法，结果为3.1。我这一举动虽然失败了，但是仔细观察发现，我算到了π的小数点后一位，说明我的得数没问题，但是位数太少。我总结了这一次算π失败的原因：1、测量工具不给力；2、自己读数不精确；3、方法错误。

        接下来，我在课外书中无意中得知祖冲之求出了密率和约率：密率355/113；约率22/7。我就开始求这两个分数的分数值。这一次还算成功，约率是3.142857142857. . .而密率我只是算到3.1415929。但是我又发现了问题：π是无理数，但约率却是循环小数，而密率算到3.1415929中的这个“9”我就发现问题啦：据我所知π≈3.1415926，而在本来应该是6的地方直挺挺地站着“9”。这一次算是向成功完成了一个较大的飞跃。看来，我必须在方法上有所改变了。

       我开始检阅各种书目，发现了更多计算方法。

        从最早的规律——圆的周长为3，直径就为1开始，不只是普通人，就连不少数学家都认为π=3。

        数学家认为π=3的这种状况，一直持续到三国时期魏晋数学家刘徽使用割圆术，如下图：

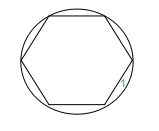
计算出π=3.14，接的是正192边形。而在这之前，人们都用6边形周长代替圆的周长，这样做误差太大，而在圆内接的正边形中，边越多，π值的误差就越小。

   而在魏晋南北朝时期，中国又出了一位大数学家——祖冲之。他算出了密率355/113和约率22/7，并且得出3.1415927>π>3.1415926，这是人类数学史上的重大突破。

         1650年，英国数学家沃利斯利用类比、归纳和极限的方法，从计算圆的面积入手，得出：π/4=2*4*4*6*6*…/1*3*3*5*5*…。

   分析法算π的乐章开始于詹姆斯·格雷戈里得出的arctanx=x-x3/3+x5/5-x7/7+x9…（-1<x≤1）。当时如果他让x=1就能得到π值了，可惜他没有。最后，这个公式被莱布尼茨发现了，于是就被命名为“莱布尼兹公式”。

   接下来，威力强大的算π工具——电子计算机已经横空出世。电子计算机的大致过程是：先定算π公式，将它编入程序后输入计算机，再发出计算指令，最后打印出来。2002年12月6日，东京大学信息基础（IT）中心和日立制作所的联合研究小组日宣布，该中心的金田康正等，与日立制作的员工共9人合作，利用日立制作所并行超级电脑系统——日立拥有SR80001MPP主记忆体，64-弄得，耗时400多小时，算出了12411亿位π值。这个电脑通过高速通信线路连接而成，1秒钟之内完成2万亿次计算，当时计算能力居世界第26位。主要计算和验算共用约600小时，计算在11月24日完成的。这次计算改善并应用了名为“分解有理化数法”。

   从1位到2000万位，算π值是人类数学发展的代表，π是一个永无止境的数——朴实无华，却又见证着整个科学史的发展，也诱惑着人们永无止境地探索。