圆周率π的数学史 五年一班  陈家讯  王泓霖  卢华绅

                                                               圆周率π的数学史

                                              五年一班  陈家讯  王泓霖  卢华绅

       π是无限循环小数，π可以用于各个领域。在中国，刘徽曾用多边形的边数增加来试图逼近圆周率，求出π的近似值为3.1416。在印度，阿耶波多利用384边形的周长，算出圆周率约为9.8684。1615年，鲁道夫·范·科伊伦算出了小数点后32位小数。

       随着计算机的革命，在2002年时，圆周率已经被计算到小数点后12411位。古希腊数学家阿基米德发现正多边形的边数越来越多时，这个形状就越来越接近圆（如下图1）

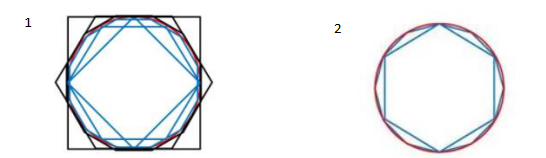
   那刘徽的割圆法又是什么呢？刘徽的割圆法就像是上面图2一样，一直算到了132边形状得出是3.14

   圆周率是一个无尽小数也是黄金分割率的来源。

   电子计算机的出现使π值计算有了突飞猛进的发展。1949年美国马里兰州阿伯丁的军队弹道研究实验室首次用计算机（ENIAC）计算π值，一下子就算到2037位小数，突破了千位数。1989年美国哥伦比亚大学研究人员用克雷－2型和IBM－VF型巨型电子计算机计算出π值小数点后4.8亿位数，后又继续算到小数点后10.1亿位数，创下最新的纪录。2010年1月7日——法国一工程师将圆周率算到小数点后27000亿位。2010年8月30日——日本计算机奇才近藤茂利用家用计算机和云计算相结合，计算出圆周率到小数点后5万亿位。

   南北朝时代著名数学家祖冲之进一步得出精确到小数点后7位的π值（约5世纪下半叶），给出不足近似值3.1415926和过剩近似值3.1415927，还得到两个近似分数值，密率355/113和约率22/7。