小学数学之圆周率的历史      五年1班   李绮蓝

                                                     小学数学之圆周率的历史

                                                         五年1班   李绮蓝

1．关于圆周率的计算是数学界一个经久不衰的话题.圆周率的最初提出是为了解决有关圆的计算而提出，随着社会的发展与科技进步，对值的计算精度越来越高.本文结合数学史课程学习及对相关文献的查阅，可知中国数学史上关于“”的演变过程：中国数学史上，圆周率最早记载于古书《周髀算经》中的古率；西汉刘歆第一个采用几何计算方法改正古率，推出=3.15146645≈3.1547；东汉的张衡第一个从理论上修正圆周率；魏晉刘徽在衡率的基础上得到 等.

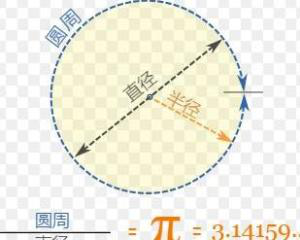
2. 圆周长度与圆的直径长度的比，圆周率的值是3.14159265358979323846…，通常用“π”表示。计算中常取3.1416为它的近似值。

3. 圆周率是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比，是精确计算圆周长、圆面积、球体积等几何形状的关键值。 在分析学里，π可以严格地定义为满足sin x = 0的最小正实数x。

        圆周率用希腊字母 π（读作pài）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值。它是一个无理数，即无限不循环小数。在日常生活中，通常都用3.14代表圆周率去进行近似计算。而用十位小数3.141592654便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。

        1965年，英国数学家约翰·沃利斯（John Wallis）出版了一本数学专著，其中他推导出一个公式，发现圆周率等于无穷个分数相乘的积。2015年，罗切斯特大学的科学家们在氢原子能级的量子力学计算中发现了圆周率相同的公式。